Problem Statement :
Given a graph which represents a flow network where every edge has a capacity. Also given two vertices source ‘s’ and sink ‘t’ in the graph, find the maximum possible flow from s to t with following constraints :
- Flow on an edge doesn’t exceed the given capacity of the edge.
- Incoming flow is equal to outgoing flow for every vertex except s and t.
For example, in following input graph,
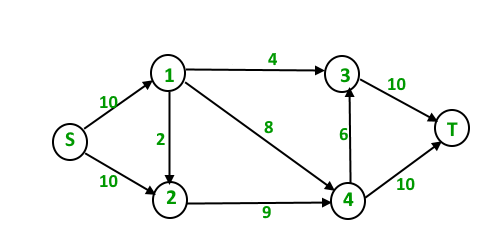
the maximum s-t flow is 19 which is shown below.
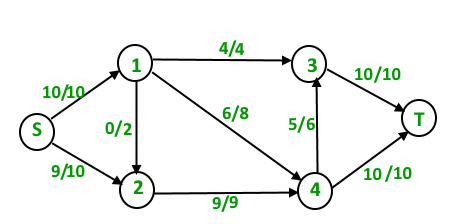

the maximum s-t flow is 19 which is shown below.

- Max Flow Problem Introduction : We introduced Maximum Flow problem, discussed Greedy Algorithm and introduced residual graph.
- Ford-Fulkerson Algorithm and Edmond Karp Implementation : We discussed Ford-Fulkerson algorithm and its implementation. We also discussed residual graph in detail.
Time complexity of Edmond Karp Implementation is O(VE2). In this post, a new Dinic’s algorithm is discussed which is a faster algorithm and takes O(EV2).
Like Edmond Karp’s algorithm, Dinic’s algorithm uses following concepts :
- A flow is maximum if there is no s to t path in residual graph.
- BFS is used in a loop. There is a difference though in the way we use BFS in both algorithms.
In Edmond’s Karp algorithm, we use BFS to find an augmenting path and send flow across this path. In Dinic’s algorithm, we use BFS to check if more flow is possible and to construct level graph. In level graph, we assign levels to all nodes, level of a node is shortest distance (in terms of number of edges) of the node from source. Once level graph is constructed, we send multiple flows using this level graph. This is the reason it works better than Edmond Karp. In Edmond Karp, we send only flow that is send across the path found by BFS.
1) Initialize residual graph G as given graph.
1) Do BFS of G to construct a level graph (or
assign levels to vertices) and also check if
more flow is possible.
a) If more flow is not possible, then return.
b) Send multiple flows in G using level graph
until blocking flow is reached. Here using
level graph means, in every flow,
levels of path nodes should be 0, 1, 2...
(in order) from s to t.
A flow is Blocking Flow if no more flow can be sent using level graph, i.e., no more s-t path exists such that path vertices have current levels 0, 1, 2… in order. Blocking Flow can be seen same as maximum flow path in Greedy algorithm discussed discussed here.
Initial Residual Graph (Same as given Graph)

Total Flow = 0

Total Flow = 0
First Iteration : We assign levels to all nodes using BFS. We also check if more flow is possible (or there is a s-t path in residual graph).
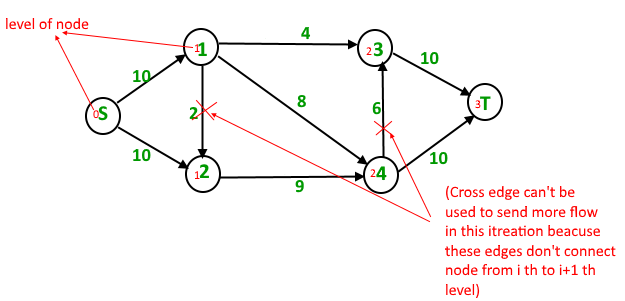

Now we find blocking flow using levels (means every flow path should have levels as 0, 1, 2, 3). We send three flows together. This is where it is optimized compared to Edmond Karp where we send one flow at a time.
4 units of flow on path s – 1 – 3 – t.
6 units of flow on path s – 1 – 4 – t.
4 units of flow on path s – 2 – 4 – t.
Total flow = Total flow + 4 + 6 + 4 = 14
4 units of flow on path s – 1 – 3 – t.
6 units of flow on path s – 1 – 4 – t.
4 units of flow on path s – 2 – 4 – t.
Total flow = Total flow + 4 + 6 + 4 = 14
After one iteration, residual graph changes to following.
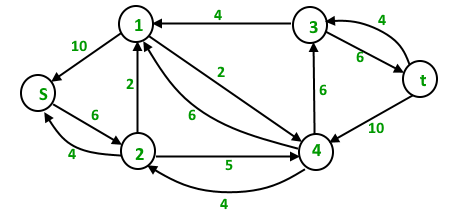
Second Iteration : We assign new levels to all nodes using BFS of above modified residual graph. We also check if more flow is possible (or there is a s-t path in residual graph).
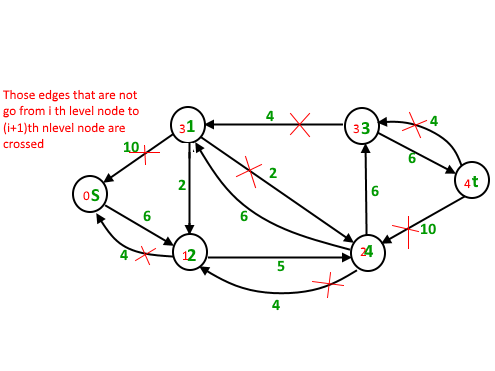
Now we find blocking flow using levels (means every flow path should have levels as 0, 1, 2, 3, 4). We can send only one flow this time.
5 units of flow on path s – 2 – 4 – 3 – t
Total flow = Total flow + 5 = 19

Second Iteration : We assign new levels to all nodes using BFS of above modified residual graph. We also check if more flow is possible (or there is a s-t path in residual graph).

Now we find blocking flow using levels (means every flow path should have levels as 0, 1, 2, 3, 4). We can send only one flow this time.
5 units of flow on path s – 2 – 4 – 3 – t
Total flow = Total flow + 5 = 19
The new residual graph is
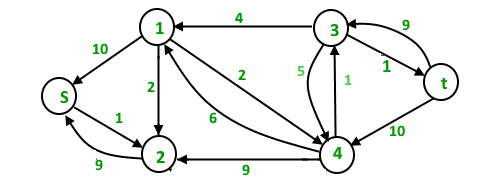

Third Iteration : We run BFS and create a level graph. We also check if more flow is possible and proceed only if possible. This time there is no s-t path in residual graph, so we terminate the algorithm.
Implementation:
Below is c++ implementation of Dinic’s algorithm:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 | // C++ implementation of Dinic's Algorithm #include<bits/stdc++.h> using namespace std; // A structure to represent a edge between // two vertex struct Edge { int v ; // Vertex v (or "to" vertex) // of a directed edge u-v. "From" // vertex u can be obtained using // index in adjacent array. int flow ; // flow of data in edge int C; // capacity int rev ; // To store index of reverse // edge in adjacency list so that // we can quickly find it. }; // Residual Graph class Graph { int V; // number of vertex int *level ; // stores level of a node vector< Edge > *adj; public : Graph(int V) { adj = new vector<Edge>[V]; this->V = V; level = new int[V]; } // add edge to the graph void addEdge(int u, int v, int C) { // Forward edge : 0 flow and C capacity Edge a{v, 0, C, adj[v].size()}; // Back edge : 0 flow and 0 capacity Edge b{u, 0, 0, adj[u].size()}; adj[u].push_back(a); adj[v].push_back(b); // reverse edge } bool BFS(int s, int t); int sendFlow(int s, int flow, int t, int ptr[]); int DinicMaxflow(int s, int t); }; // Finds if more flow can be sent from s to t. // Also assigns levels to nodes. bool Graph::BFS(int s, int t) { for (int i = 0 ; i < V ; i++) level[i] = -1; level[s] = 0; // Level of source vertex // Create a queue, enqueue source vertex // and mark source vertex as visited here // level[] array works as visited array also. list< int > q; q.push_back(s); vector<Edge>::iterator i ; while (!q.empty()) { int u = q.front(); q.pop_front(); for (i = adj[u].begin(); i != adj[u].end(); i++) { Edge &e = *i; if (level[e.v] < 0 && e.flow < e.C) { // Level of current vertex is, // level of parent + 1 level[e.v] = level[u] + 1; q.push_back(e.v); } } } // IF we can not reach to the sink we // return false else true return level[t] < 0 ? false : true ; } // A DFS based function to send flow after BFS has // figured out that there is a possible flow and // constructed levels. This function called multiple // times for a single call of BFS. // flow : Current flow send by parent function call // start[] : To keep track of next edge to be explored. // start[i] stores count of edges explored // from i. // u : Current vertex // t : Sink int Graph::sendFlow(int u, int flow, int t, int start[]) { // Sink reached if (u == t) return flow; // Traverse all adjacent edges one -by - one. for ( ; start[u] < adj[u].size(); start[u]++) { // Pick next edge from adjacency list of u Edge &e = adj[u][start[u]]; if (level[e.v] == level[u]+1 && e.flow < e.C) { // find minimum flow from u to t int curr_flow = min(flow, e.C - e.flow); int temp_flow = sendFlow(e.v, curr_flow, t, start); // flow is greater than zero if (temp_flow > 0) { // add flow to current edge e.flow += temp_flow; // subtract flow from reverse edge // of current edge adj[e.v][e.rev].flow -= temp_flow; return temp_flow; } } } return 0; } // Returns maximum flow in graph int Graph::DinicMaxflow(int s, int t) { // Corner case if (s == t) return -1; int total = 0; // Initialize result // Augment the flow while there is path // from source to sink while (BFS(s, t) == true) { // store how many edges are visited // from V { 0 to V } int *start = new int[V+1]; // while flow is not zero in graph from S to D while (int flow = sendFlow(s, INT_MAX, t, start)) // Add path flow to overall flow total += flow; } // return maximum flow return total; } // Driver program to test above functions int main() { Graph g(6); g.addEdge(0, 1, 16 ); g.addEdge(0, 2, 13 ); g.addEdge(1, 2, 10 ); g.addEdge(1, 3, 12 ); g.addEdge(2, 1, 4 ); g.addEdge(2, 4, 14); g.addEdge(3, 2, 9 ); g.addEdge(3, 5, 20 ); g.addEdge(4, 3, 7 ); g.addEdge(4, 5, 4); // next exmp /*g.addEdge(0, 1, 3 ); g.addEdge(0, 2, 7 ) ; g.addEdge(1, 3, 9); g.addEdge(1, 4, 9 ); g.addEdge(2, 1, 9 ); g.addEdge(2, 4, 9); g.addEdge(2, 5, 4); g.addEdge(3, 5, 3); g.addEdge(4, 5, 7 ); g.addEdge(0, 4, 10); // next exp g.addEdge(0, 1, 10); g.addEdge(0, 2, 10); g.addEdge(1, 3, 4 ); g.addEdge(1, 4, 8 ); g.addEdge(1, 2, 2 ); g.addEdge(2, 4, 9 ); g.addEdge(3, 5, 10 ); g.addEdge(4, 3, 6 ); g.addEdge(4, 5, 10 ); */ cout << "Maximum flow " << g.DinicMaxflow(0, 5); return 0; } |
Output:
Maximum flow 23
Time Complexity : O(EV2). Doing a BFS to construct level graph takes O(E) time. Sending multiple more flows until a blocking flow is reached takes O(VE) time. The outer loop runs at-most O(V) time. In each iteration, we construct new level graph and find blocking flow. It can be proved that the number of levels increase at least by one in every iteration (Refer the below reference video for the proof). So the outer loop runs at most O(V) times. Therefore overall time complexity is O(EV2).



5 Comments
Good information mate
ReplyDeleteGreat post, hadn't heard about Dinic's algorithm before.
ReplyDeleteBtw, there a typo in the second figure. The in-flow to t is 20, where the upper in-edge should have 9/10.
Nice Article. 123movies Thank you very much for sharing this awesome post with us. Keep Posting.
ReplyDeleteVery nice post! Very informative. Visit @ Android App Development Company in Delhi
ReplyDeleteThank you very nice sharing.
ReplyDelete